Để mô tả các đặc điểm hình học của một tinh thể, 5 thuật ngữ sau thường được phân biệt: hệ thống pha lê, lớp tinh thể, thói quen, hình thức, và song tinh.
Những khái niệm này lần lượt được dựa trên các khái niệm về đơn vị tế bào và mạng lưới điểm.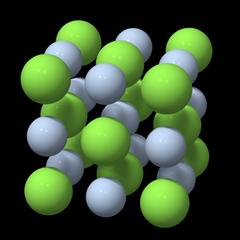
Tế bào đơn vị và mạng lưới điểm
Trong một tinh thể, các phân tử và nguyên tử được sắp xếp theo cách cố định, tạo thành một khối có đặc điểm hình học cụ thể (ví dụ muối ăn, natri clorua, các khối nhỏ). Các nguyên tử trong một tinh thể tạo thành một mạng lưới ba chiều ảo. Khối xây dựng nhỏ nhất của lưới điện này phản ánh thuộc tính hình học và tính đối xứng của tinh thể đó là đơn vị tế bào . Bảng muối có một tế bào đơn vị gồm 13 natri và 14 nguyên tử clo tạo thành một khối hoàn hảo (3: 3: 3, như được thể hiện trong hình , với chlorine được biểu tượng bằng quả bóng màu xanh lá cây, và natri bằng các màu xám xanh [1]). Mối quan hệ của natri với clo trong muối ăn là 1: 1, vậy nên hiển nhiên là một tế bào đơn vị không nhất thiết phản ánh công thức hóa học. Lý do là các đơn vị lân cận có các nguyên tử chung nhau nằm trên các cạnh và góc của chúng.
Và vì cùng một lý do như vậy là sai khi nghĩ đến các tế bào đơn vị như gạch hình thành một tinh thể [2], tế bào đơn vị chỉ là một khái niệm hình học trừu tượng.
Các cạnh của một ô đơn vị tương ứng với các trục trong lưới ba chiều [3]. Lưới này được gọi là lưới điểm, là một khái niệm trừu tượng. Mối liên hệ giữa ô đơn vị, trục mạng, và mạng tinh thể được mô tả trong hình 2, với một tế bào đơn vị được làm nổi bật. Hệ tinh thể tinh thể hoặc không gian là hệ tọa độ được sử dụng để xác định các dạng tinh thể (xem bên dưới). Mặt tinh thể được đặt tên theo vị trí tương đối của chúng đến hệ tọa độ đó.
Hệ thống tinh thể
Các góc giữa các trục của mạng lưới điểm và chiều dài tương đối của các cạnh của tế bào đơn vị được sử dụng để xác định các hệ tinh thể khác nhau. Mỗi khoáng vật (ngoại trừ khoáng vô định hình) thuộc một trong 7 hệ tinh thể (hoặc 6, vì đôi khi hệ thống hình tam giác/ tứ giác và hệ lục giác được nhóm lại với nhau). Bảng dưới đây cho biết tổng quan ngắn.
| Góc |
Trục |
Hệ thống tinh thể |
| α = β = γ = 90° |
a = b = c |
Cubic hay Isometric |
| α = β = γ = 90° |
a = b , c ≠ a , c ≠ b |
Tetragonal |
| α = β = γ = 90° |
a ≠ b ≠ c |
Orthorhombic |
| α = β = γ ≠ 90° |
a = b = c |
Tam giác hay tứ giác |
| α = β = 90° , γ = 120° |
a = b , c ≠ a , c ≠ b |
Lục giác |
| α ≠ β ≠ γ , β = 90° |
a ≠ b ≠ c |
Monoclinic |
| α ≠ β ≠ γ ≠ 90° |
a ≠ b ≠ c |
Triclinic |
Thạch anh thuộc hệ tinh thể tam giác [4]. Một ô đơn vị tam giác trông giống như một khối lập phương nghiêng – chiều dài của tất cả các trục a, b, và c bằng nhau, và các góc ở các góc tương ứng đều bằng nhưng không có hình chữ nhật. (Hình 3).
Nhưng mặc dù thạch anh thuộc về hệ thống tam giác, tế bào đơn vị của nó là lục giác.
Vậy nên, khi mô tả tinh thể thạch anh, thuật ngữ được dùng là một trong những cách để mô tả các tinh thể hình lục giác (Hình 4).:
Bốn trục được phân biệt, a1, a2, a3, và c . Tất cả trục a có chiều dài bằng nhau và nằm trong một mặt phẳng, với góc 120 ° giữa chúng. Khi đề cập đến tất cả trong số họ hoặc một trong số họ và nó không quan trọng mà người ta, người ta sử dụng các biểu tượng a0 hoặc chỉ đơn giản là a. Các c trục chạy vuông góc với a0 . Chiều dài của nó là khác nhau từ trục a, với thạch anh nó là 1.100 lần chiều dài của a0.
Hình 5 miêu tả mối quan hệ giữa đối xứng lục giác và tế bào đơn vị lục giác. Một tế bào đơn vị lục giác không phải là một lăng kính lục giác, nó là một hình thoi.
Một tế bào đơn vị bậc ba cũng có thể được xác định bằng tọa độ lục giác – các trục lục giác dễ dàng được chiếu vào ô đơn vị (Hình 6). Điều này cũng hữu dụng với một khối hoàn hảo, và nếu bạn nhìn vào một hình lập phương từ đúng góc, bạn sẽ thấy một hình lục giác là phác thảo của nó.
Lớp pha lê hoặc đối xứng
Thuật ngữ “lớp tinh thể” đề cập đến các thuộc tính đối xứng quay và đảo ngược của lưới tinh thể khoáng. Mỗi loại khoáng (trừ những loại vô định hình) thuộc một trong 32 lớp đối xứng.
thạch anh là thành viên của lớp 32 , hình tam giác-tam giác – có nghĩa là “ba – hai”, không phải là ba mươi hai. “32” là biểu tượng được gọi là Hermann-Maugin, chỉ ra rằng thạch anh có một đối xứng xoay 3 lần đối xứng một và một đối xứng quay hai chiều trên một trục khác .
Khái niệm đối xứng gương có liên quan đến khái niệm thuận tay trái hoặc vô định hình. Một tế bào đơn vị có thể thiếu đối xứng gương: trong trường hợp đó, nếu bạn phản xạ các tọa độ nguyên tử xung quanh một trục, các vị trí không khớp nhau. Như một đơn vị tế bào- và kết quả là toàn bộ tinh thể – hoặc là trái hoặc phải, tương tự như tay trái và tay phải của chúng tôi.
Mẫu pha lê
Thuật ngữ “dạng tinh thể” hơi gây chút hiểu nhầm, bởi vì nó không nói gì về hình dạng thực sự của tinh thể. Một dạng tinh thể là một khối học ảo được bao quanh bởi các mặt phẳng lattice với các tính đối xứng giống hệt nhau.
Bạn có thể nghĩ máy bay mạng là cắt trực tiếp thông qua một mạng lưới. Hình 7 cho thấy một cái nhìn hai chiều của một mạng lưới natri clorua [5] , với các đường mỏng là các biên của các tế bào đơn vị. Các đường màu cam và vàng là những mặt phẳng tinh thể có dạng hình kim cương. Tất nhiên, có nhiều cách để cắt qua một lưới, và để được một hình dạng tinh thể hợp lệ, các máy bay cần phải chạy qua các điểm mạng – góc các tế bào đơn vị. Ngoài ra, chỉ những máy bay mạng có tính chất đối xứng giống hệt nhau được sử dụng ở một dạng. Trong một khối lưới, với một đơn vị tế bào khối, hình thức cơ bản nhất là một khối lập phương.

Hình 8 cho thấy một vài hình thức có thể trong một lưới hai chiều. Hình thoi với đường nét phác hoạ không phải là một hình thức hợp lệ, bởi vì nó không được bao quanh bởi các mặt phẳng mạng với các thuộc tính đối xứng giống hệt nhau với mặt lưới bên dưới (một mặt phẳng cho thấy đối xứng gương trong khi không có mặt trong đó có 3 nguyên tử Trong khi phần còn lại là 5).
Tất cả các mặt của một dạng tinh thể trong một lưới ba chiều đều có hình dạng giống nhau, ví dụ như tất cả đều là các hình vuông hoặc hình tam giác. Trong các lớp tinh thể nhất định, một số dạng không phải là “hoàn thiện”, nhưng mở ở một hoặc hai đầu, và được gọi là các hình thức mở (ví dụ như tất cả lăng kính), trái ngược với các dạng hoàn chỉnh, được gọi là các hình thức đóng kín , một hình khối là một ví dụ [6] .
Hình dạng thực sự của một tinh thể có thể được xem như là sự kết hợp của các hình thức giao nhau. Hình dạng do đó phụ thuộc cả về sự có mặt và kích thước của các dạng tinh thể khác nhau. Tinh thể trông rất khác (ví dụ như một cái được kéo dài ra và mặt kia là hình lăng trụ ngắn) vẫn có thể cho thấy cùng một dạng tinh thể.
Do mối quan hệ này, thuật ngữ “dạng tinh thể” đôi khi còn dùng để chỉ các loại mặt tinh thể mà có thể nhìn thấy trên tinh thể. Tinh thể với các loại tinh thể khác nhau có mặt trên chúng được cho là có dạng khác [7] .
Trong nhiều hình thức có thể biểu hiện như khuôn mặt trên tinh thể phụ thuộc vào các chi tiết cấu trúc cố hữu và các điều kiện môi trường trong quá trình phát triển. Ví dụ, trong khi bạn có thể nghĩ đến việc cắt qua mạng lưới natri natri clorua như thể hiện trong hình 9, tương ứng với hình dạng viên kim cương ở hình. 8, bạn sẽ không bao giờ nhìn thấy một hình thức như vậy trên một viên đá muối đá trong tự nhiên. Trong khi pha lê phát triển trong dung dịch nước, một chiếc máy bay làm từ các ion chlorine có điện tích sẽ thu hút các ion natri tích điện dương và sẽ nhanh chóng phát triển thành một góc bình thường của khối lập phương. Dạng tinh thể này là nhiệt động lực học không ổn định trong muối đá. Các gương mặt của một khối lập phương cân bằng về điện tử và có xu hướng phát triển và hoà tan chậm hơn trong dung dịch nước (chúng ổn định hơn) và vì vậy chúng là dạng tinh thể được ưu tiên trong muối đá.
Một dạng trong muối đá có thể ổn định ở các khoáng chất khác của hệ tinh thể khối có cấu trúc bên trong khác nhau, như florit hoặc garnet. Một số khoáng chất thích mặc quần áo giống nhau mỗi ngày, như muối đá, những thứ khác cho thấy nhiều dạng và hình dạng khác nhau đáng kinh ngạc, khác với điều kiện tăng trưởng, như pyrit, florit hoặc với khoảng 200 dạng khác nhau và hơn 1000 kết hợp được biết, calcit .
Có một thuật ngữ toán học để mô tả các dạng tinh thể, gọi là các chỉ số Miller cho các hệ thống tinh thể với ba trục và phần mở rộng cho các hệ thống tinh thể với bốn trục, chỉ số Miller-Bravais. Chú thích véc tơ được sử dụng trong thuật ngữ này (ví dụ: {1 0 1 1} cho dạng tứ diện r trong thạch anh) mô tả chính xác mối quan hệ của các dạng với mạng lưới tinh thể bên dưới. Một lời giải thích giới thiệu về danh pháp khó xử này đang chuẩn bị, nhưng trong khi đó tôi phải hướng bạn tới các trang web khác và sách giáo khoa về khoáng vật học để đưa vào chủ đề khá phức tạp và trừu tượng này:
Kết đôi
Một tinh thể được cho là được ghép nối nếu nó gồm có 2 hoặc nhiều cá thể tinh thể có mạng lưới tinh thể được định hướng khác nhau nhưng vẫn được trồng xen kẽ theo một cách thức cụ thể. Các cá thể đơm không chỉ được đặt cùng nhau ở một góc tùy ý; chúng chia nhau các nguyên tử dọc viền của họ. Đối với trường hợp này, viền luôn luôn tương ứng với dạng pha lê cụ thể: nó cắt mạng lưới tinh thể của các cá thể riêng ở cùng một góc độ và các cá thể đó chạm vào nhau như thể hai tinh thể riêng biệt chạm vào nhau với các mặt tinh thể giống hệt nhau. Mặt phẳng ảo tương ứng với các mặt tinh thể này được gọi là mặt phẳng thành phần.
Đối với lưới tinh thể, có thể thực hiện được hai loại hoạt động hình học để có được một tinh thể kết hợp:
- Xoay quanh một trục tinh thể, trục cặp
- Phản chiếutại một mặt phẳng tinh thể, mặt phẳng kết đôi.
Vậy nên, mỗi luật kết đôi được xác định bởi các loại hoạt động hình học và máy bay hay mặt phẳng tinh thể cụ thể. Các trục song song và các mặt phẳng không phải trùng khớp với các trục tinh thể chính.
Lưu ý rằng ngay cả khi cặp song sinh có một trục song song và không phải là một mặt phẳng song song, nó vẫn có một mặt phẳng ghép.
Một điểm khác biệt nữa là cặp song sinh thâm nhập và liên hệ với cặp song sinh:
- Trong một cặp tiếp xúc (Hình.10, trên cùng), đường biên giữa các cá thể con trùng với mặt phẳng thành phần.
- Trong một cặp thâm nhập (Hình.10, đáy) biên giới giữa các cá thể riêng có hình dạng bất thường. Vẫn có một mặt phẳng kết cấu ảo được xác định cho những cặp song sinh này, vì các cá thể con người vẫn hướng vào nhau theo một góc độ cụ thể.
Trái ngược với niềm tin chung, các thuật ngữ liên hệ với cặp song sinh và cặp đôi thâm nhập không xác định xem các cá thể dưới có thể nhìn thấy ở dạng vĩ mô hay không.
Về mặt lý thuyết, có nhiều luật song tinh kết nghĩa khác nhau dưới dạng các dạng tinh thể, nhưng trong tự nhiên chỉ có rất ít người thực sự có thể được quan sát thấy trong một loài khoáng. Ví dụ, thạch anh chỉ có ba loại cặp song sinh thường xuyên được tìm thấy.
Các tinh thể kết tinh tương tự có thể giống như cặp sinh đôi đối với hầu hết mọi người, nhưng trong đa số trường hợp, chúng không phải là cặp song tinh
Thói quen pha lê
“Thói quen pha lê” dùng để chỉ hình dạng tổng thể của tinh thể, để lại cấu trúc trơ.
Thói quen pha lê có thể được mô tả bằng các thuật ngữ rõ ràng như “như thùng”, “như kim”, “dài”, hoặc “lăng trụ ngắn”.
Tuy nhiên, khái niệm thói quen pha lê cũng bao gồm các thuật ngữ ít phổ biến hơn là “thói quen tam diện” hoặc các thuật ngữ đặc trưng cho từng loại khoáng, như “thói quen Dauphiné”. Thói quen của một tinh thể phụ thuộc vào kích thước tương đối của khuôn mặt tinh thể. Ví dụ, sự thống trị của các dạng nhất định trên một viên pha lê thạch anh có thể gây ra một hình dạng giống như hình khối, được gọi là “thói quen giả tạo giả”.
Lưu ý:
Người ta cũng có thể sử dụng thuật ngữ “thói quen” để mô tả sự xuất hiện chung của khoáng, trái ngược với một tinh thể đơn. Thuật ngữ điển hình trong ngữ cảnh đó là “druzy”, “compact”, “dendritic”, “fibrous”, hoặc “granular”.
Again, Thông tin thêm, Văn học, Liên kết
Bất kỳ sách giáo khoa về khoáng vật sẽ thảo luận về chủ đề này một cách rộng rãi.
Bất kỳ sách giáo khoa về khoáng vật sẽ thảo luận về chủ đề này một cách rộng rãi.
Một lần nữa, tôi xin đề nghị giải thích rất tốt đẹp có thể được tìm thấy tại trang web này:Giới thiệu về tinh thể học và Hệ thống tinh thể khoáng.
Chú thích
- Không có khoảng cách giữa các nguyên tử, nhưng để hình dung mối quan hệ hình học của chúng, tôi đã để lại một khoảng trống giữa chúng.Nếu chúng ta thực sự có thể nhìn thấy các nguyên tử, chúng có thể trông giống như một quả cầu có nhiều mây mà không có đường viền hoặc bề mặt rõ ràng, những đám mây bao gồm những electron chuyển động nhanh.
- Mặc dù khi René Chỉ Haüy nảy ra ý tưởng của tế bào đơn vị năm 1784, ông đã thực sự suy nghĩ các tế bào đơn vị như gạch cơ bản để hình thành một tinh thể.
- Thông thường 3 trục, nhưng tế bào đơn vị lục giác là một ngoại lệ, nó có 4 trục tạo thành một lưới ba chiều.
- Một số tác giả đưa thạch anh vào hệ tinh thể lục giác.Không có gì sai với điều đó, chỉ là họ chọn phân biệt 6 hệ tinh thể và coi hệ thống tam giác là một trường hợp đặc biệt của hệ lục giác. Các đơn vị tế bào của thạch anh không phải là tam diện, mà là lục giác.
- Để chứng minh nó trong một mạng lưới thạch anh là rất khó hiểu vì cấu trúc rất phức tạp và vì cùng một lý do vượt quá khả năng kỹ thuật của tôi.
- Một hình thức không phải là một khối ba chiều, nó có thể là một máy bay hai chiều đơn giản.
[7] Ở Đức, có một thuật ngữ thích hợp với thực tế là hai tinh thể có khuôn mặt tinh thể tương đương: chúng được cho là có cùng một “Tracht”, là một biểu hiện thời trang cho quần áo. Cũng có thể có một biểu hiện tương ứng bằng tiếng Anh mà tôi không biết.
– Phạm Thị Hòa dịch















